| |




Le funzioni di veritÓ possono ordinarsi in
delle serie.
Ecco il fondamento della teoria della probabilitÓ.
5.101 Le funzioni di veritÓ d'ogni numero di proposizioni
elementari possono scriversi in uno schema della seguente specie:
| (V V V V)(p, q) |
Tautologia (se p allora p, e se q allora q)
(p 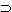 p . q p . q 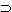 q) q) |
| (F V V V)(p, q) |
in parole: non e p e q.
(~(p . q)) |
| (V F V V)(p, q) |
'' '' se
q allora p. (q 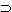 p) p) |
| (V V F V)(p, q) |
'' '' se
p allora q. (p 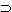 q) q) |
| (V V V F)(p, q) |
'' '' p
o q. (p v q) |
| (F F V V )(p, q) |
'' '' non
q. (~q) |
| (F V F V)(p, q) |
'' '' non
p. (~p) |
| (F V V F)(p, q) |
'' '' p
o q, ma non entrambi.(p . ~q :v: q . ~p) |
| (V F F V)(p, q) |
'' '' se
p, allora q; e se q, allora p.
(p  q) q) |
| (V F V F)(p, q) |
'' '' p |
| (V V F F)(p, q) |
'' '' q |
| (F F F V)(p, q) |
'' '' nÚ
p nÚ q. (~p . ~q , o
anche: p | q) |
| (F F V F)(p, q) |
'' '' p
e non q. (p . ~q) |
| (F V F F)(p, q) |
'' '' q
e non p. (q . ~p) |
| (V F F F)(p, q) |
'' '' p
e q. (p . q) |
| (F F F F)(p, q) |
Contraddizione (p e non p; e q e non
q.)
(p . ~p . q . ~q) |
Quelle possibilitÓ di veritÓ degli argomenti di veritÓ della proposizione
le quali la verificano, le chiamer˛ i fondamenti di veritÓ della
proposizione.
5.11 - 5.15
|